Tags: #AI

References:
Graph Convolutional Networks —Deep Learning on Graphs
Smarter.ai - Graph Convolutional Networks: Implementation in PyTorch
Notes for Stanford CS224W

Basic Concepts

$G(N,E)$: The graph $G$ with nodes $N$ and edges $E$.

For Undirected graph, we define the node degree $k_i$ of node $i$ as the number of edges adjacent to node $i$. The average degree is:

For Directed graphs have directed links (e.g. following on Twitter). We define the in-degree $k_i^{in}$ as the number of edges entering node $i$. Similarly, we define the out-degree $k_i^{out}$ as the number of edges leaving node $i$. The average degree is then

Introduction

We've worked on graph classification, node classification, link prediction, community detection, graph embedding, and graph generation. These involve predicting a graph's class, classifying nodes, predicting connections, clustering nodes, preserving information in a vector, and generating new graphs.

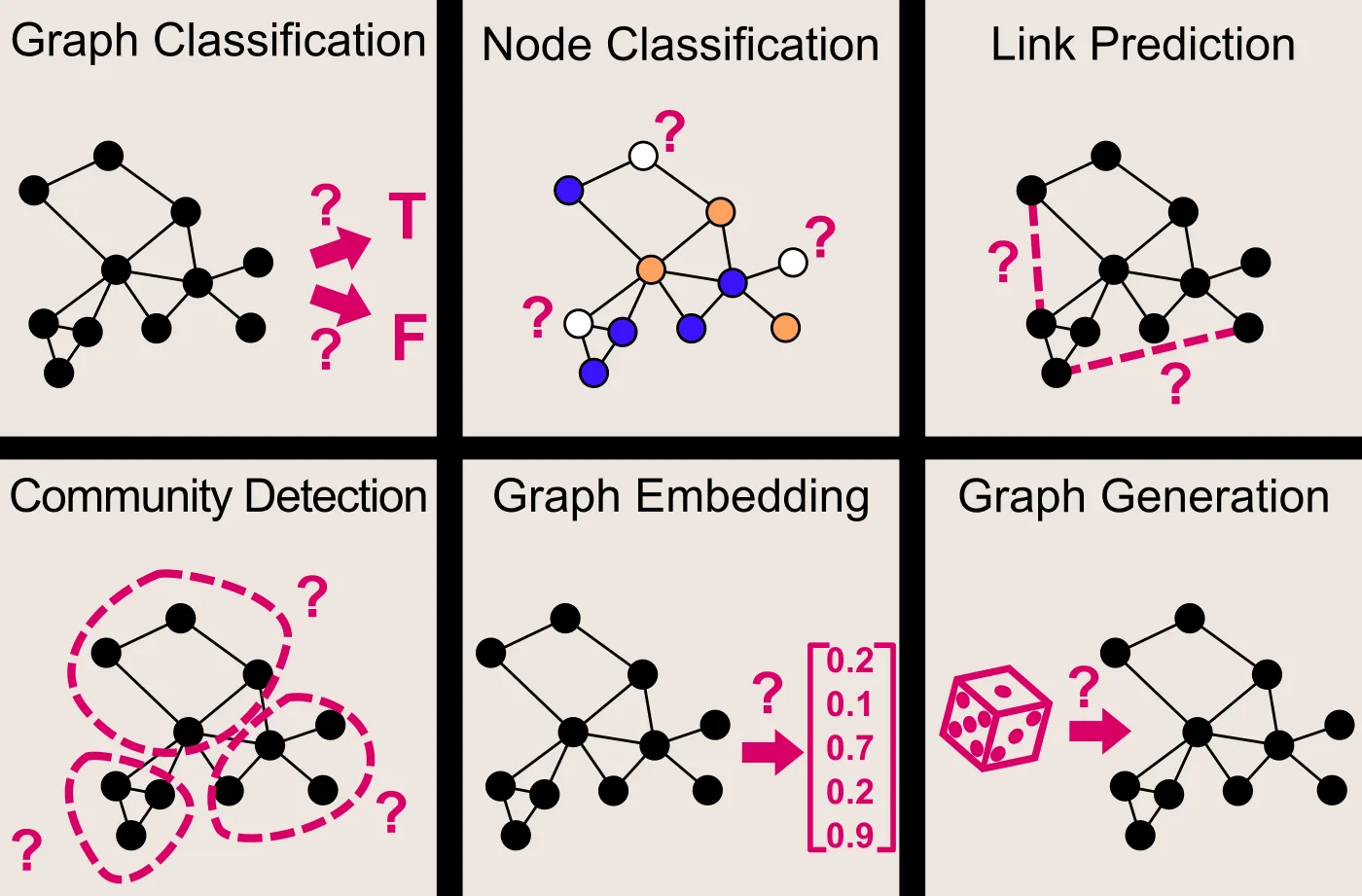
Traditional convolutional methods in graphs is meaningless.
⇒ Graph convolution

Definition & Methods

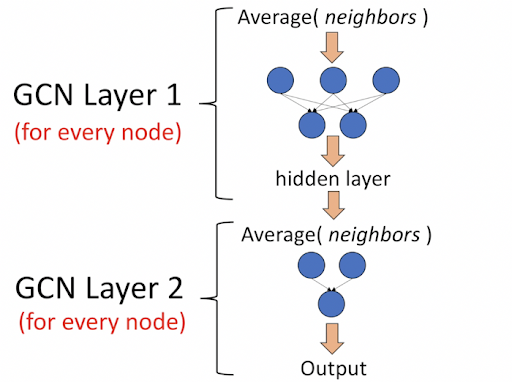
In the case of a GCN, the inputs are:

• $N\times C$ array, for each of the $N$ nodes of the graph, $C$ features.
• $N\times N$ adjacency matrix.

GCN Operation

From Zotero: Semi-Supervised Classification with Graph Convolutional Networks

• $x$: A vector representing the features of a node in the graph.
• $g$: The graph structure, represented as an adjacency matrix. The $(i,j)$ entry of the matrix is $1$ if there is an edge from node $i$ to node $j$ in the graph, and $0$ otherwise.
• $U$: The matrix of eigenvectors of the graph Laplacian matrix $L$, which is defined as $L=D-g$, where $D$ is the diagonal matrix of node degrees.
• $\hat{g}(\mathrm{\Lambda })$: This is a diagonal matrix of the eigenvalues of the Laplacian matrix $L$.
• $x^{\prime }$: The output of the GCN operation, which is a transformed version of the input features $x$.

GCN Layer

• ${\mathbf{x}}_i^{(k)}$ is the representation of node $i$ at iteration $k$. This is the updated node representation that we are computing.
• $\mathcal{N}(i)\cup i$ is the set of neighbors of node $i$, including itself. This is the neighborhood of node $i$ that we consider in the GCN layer.
• $\mathrm{deg}(i)$ and $\mathrm{deg}(j)$ are the degrees of nodes $i$ and $j$, respectively. The degree of a node is the number of edges incident on it (edged directly connected to a node). The term $\sqrt{\mathrm{deg}(i)}\cdot \sqrt{\mathrm{deg}(j)}$ is a normalization factor that ensures that the updates are scaled appropriately based on the degrees of the nodes. This is known as the symmetric normalization.
• $\mathbf{W}$ is a weight matrix that is learned during training. This matrix is used to transform the feature representations of the nodes.
• ${\mathbf{x}}_j^{(k-1)}$ is the representation of node $j$ at iteration $k-1$. This is the previous iteration's node representation.
• ${\mathbf{W}}^{\mathrm{\top }}\cdot {\mathbf{x}}_j^{(k-1)}$ is the transformed representation of node $j$ at iteration $k-1$. This is the result of applying the weight matrix $\mathbf{W}$ to the node representation.
• $\frac{1}{\sqrt{\mathrm{deg}(i)}\cdot \sqrt{\mathrm{deg}(j)}}\cdot ({\mathbf{W}}^{\mathrm{\top }}\cdot {\mathbf{x}}_j^{(k-1)})$ is the contribution of node $j$ to the updated representation of node $i$. This term represents the normalized message sent from node $j$ to node $i$.
• $\sum _{j\in \mathcal{N}(i)\cup i}\frac{1}{\sqrt{\mathrm{deg}(i)}\cdot \sqrt{\mathrm{deg}(j)}}\cdot ({\mathbf{W}}^{\mathrm{\top }}\cdot {\mathbf{x}}_j^{(k-1)})$ is the sum of the normalized messages sent from all neighbors of node $i$, including itself. This sum represents the aggregated information from the neighborhood of node $i$.
• $\mathbf{b}$ is a bias term that is learned during training. This term is added to the aggregated information to produce the final updated representation of node $i$.

ChebConv

From Zotero: Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering
However, without further assumptions, such a filter does not have a compact support, and moreover learning all the components of $\hat{g}(\mathrm{\Lambda })$ has $O(N)$ complexity. To fix both issues, we will use instead a polynomial parametrization of $\hat{g}$ of degree $K$:

This reduce the learning complexity to $O(K)$.
$\hat{g}$ is $K$-localized ⇒ e.g. the value at node $j$ of $\hat{g}$ centered at node $i$ is $0$ if the the minimum number of edges connecting two nodes on the graph is greater than $K$.
$K=1$ ⇒ $3\times 3$ convolutional filters.

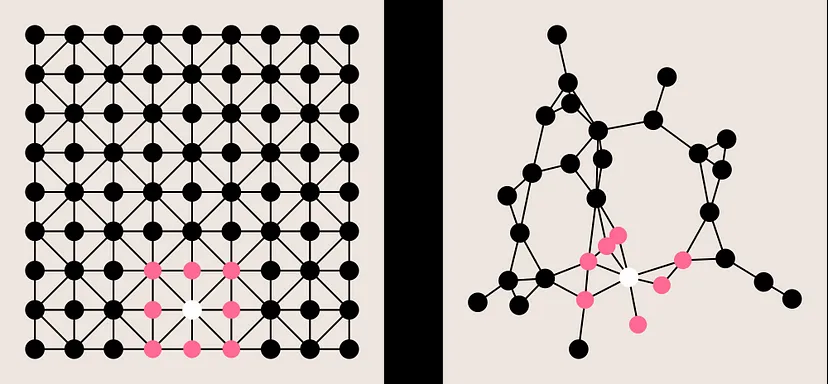
Related Works

PyG

pyg-team/pytorch_geometric: Graph Neural Network Library for PyTorch